HISTOIRE ABREGEE DES CODES SECRETS
 Que le lecteur se rassure, il ne s’agira pas d’une enième histoire des codes secrets, du déchiffrement ou de cryptographie. Il nous faut toutefois comprendre dans quel contexte l’auteur du manuscrit a pu crypter plus de 250 pages et élaborer un système relativement cohérent d’écriture.
Que le lecteur se rassure, il ne s’agira pas d’une enième histoire des codes secrets, du déchiffrement ou de cryptographie. Il nous faut toutefois comprendre dans quel contexte l’auteur du manuscrit a pu crypter plus de 250 pages et élaborer un système relativement cohérent d’écriture.
De nombreuses perspectives s’offrent à nous : il pourrait s’agir d’un texte totalement anagrammique, d’un substitution simple, d’une substitution simple en ôtant les voyelles ou les lettres doubles dans un mot.
L’histoire de l’écriture a été riche en événements cryptographiques parce qu’elle est liée au secret et au pouvoir, pouvoir politique ou pouvoir ecclésiastique. Les systèmes d’écriture jusqu’au XIXè siècle étaient nombreux, compliqués dans certains cas, mais pas forcément complexes : la science du secret n'était pas encore très développée.
Il y a deux façons d’aborder le texte : le considérer comme un texte crypté puis substitution des lettres ou une autre forme de cryptographie, sur une méthode plus ou moins connue, ou s’agit-il d’un alphabet créé avec son propre référentiel. Dans les deux cas, si l’on considère que livre a un sens, il y aura substitution des lettres pour abouter du sens caché au sens clair.
Nous partons du principe ici que les 260 pages ont été écrites avec un sens global. S’il s’agit d’une recette d’élixir de longue vie, nous savons qu’il n’existe pas Le décrire peut être compris dans la simple lecture des mots respectant une logique grammaticale cohérente avec notre langue, maisle sens des phrases décrivant les étapes de création de cet élixir pourrait être quant à lui très hermétique avec des formulations alchimiques ou à la rigueur clair, mais sans que la suite des phrases lues ne puissent dans la compréhension. Dire la phrase suivante que « l’écriture est un soleil vert qui compose » a une forme de sens qui est celui des mots et du respect de la construction syntaxique de la phrase. Par contre le sens global (enlevé de tout sens supposé poétique), n’a aucun sens puisque les mots reliés entre eux n’en ont pas. C’est aussi sur ces bases que doit s’organiser notre réflexion.
Le terme cryptographie que nous employons volontairement, dans ses racines étymologiques, signifie texte caché, et donc la sciences des écritures secrètes. Il y a donc une volonté de masquer le texte afin qu’il ne puisse être lu par celui qui n’en est pas le destinataire ou qui n’a pas la clef de déchiffrement.
La substitution dans plusieurs versets du Livre de Jéremie, du mot « sheshak » à celui de « Babel » est une transformation dans laquelle chaque lettre de l’alphabet hébreu est remplacée par celle qui a la même position que si l’on récite l’alphabet à l’envers. Il s’agit là d’un simple « jeu » linguistique et symbolique.
La dissimulation dans la scytale lacédémonienne consistait à écrire un texte sur un ruban de papyrus enroulé autour d’un axe d’un diamètre précis. Le texte envoyé était ensuite détaché de son support, et seul le lecteur connaissant le diamètre du premier support pouvait enrouler les rubans de papyrus autour d’un axe de diamètre similaire, et ainsi que la succession des mots ait qui apparaissent une fois que les rubans sont enroulés ait un sens.

Les premiers codes ont été ceux de César qui a instauré le chiffrement par substitution simple que nous verrons par la suite. Ce n’est qu’à la Renaissance que le chiffre, c’est à dire, les méthodes pour crypter, reprend de la vigueur, et reste l’apanage des grandes villes italiennes se partageant le pouvoir. Les grandes règles sont établies à cette période. Gabriel Lavinde, entre 1375 et 1383, qui fut secrétaire du Pape, élabore dans son livre « liber zifforum » le premier manuel du chiffre à l’usage des agents diplomatiques.
Dans l’empire musulman, au IXe siècle de notre ère, Al-Kindi est le premier à décrire les techniques de déchiffrement par l’analyse des fréquences. En 1987 est retrouvé à Istambul son livre intitulé « Manuscrit sur le déchiffrement des messages cryptographiques ».Cette technique d’analyse des fréquences sera utilisée seulement en occident qu’à partir du XIXe siècle.
La méthode de Jérôme CARDAN (1501-1576) consistait à écrire un texte quelconque sur une feuille, et d’appliquer par-dessus une seconde feuille contenant des fenêtres de la taille d’une lettre. En appliquant la seconde sur la première, seules les lettres apparaissant dans les fenêtres donnaient un message clair.
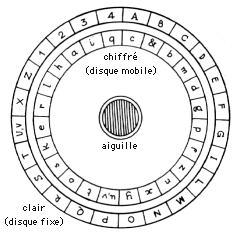
L’architecte Leo Battista Alberti (XVe siècle) construit le premier appareil de substitution. Il se compose de deux disques en cuivre (p.40 STERN), l’un fixe, et le second, plus petit, est mobile. Le plus grand disque sur sa circonférence est marqué d’un alphabet ordonné. Sur le plus petit, l’alphabet, sur sa circonférence est désordonné. On a ainsi une lecture directe pour la substitution.
Au XVIe siècle, Blaise de Vigenere invente la substitution à double clef , et Jérôme Cardan, au cours de cette même période invente le procédé de transposition.
La cryptographie connaît une grande diffusion pendant la Renaissance. C’est une science fondée sur les mathématiques ET la linguistique.
En Angleterre, Gifford, un conseiller de Marie Stuart, créa un alphabet qui était plus qu’une substitution alphabétique : il était constitué de 23 symboles qui remplaçait les lettres de l’alphabet (à l’exception de j, v et w) et 36 symboles représentant des mots ou des phrases. (P.53 SINGH). Le texte ainsi produit pourrait ressembler étrangement à la manière dont est fait le manuscrit Voynich. Pour les symboles, leur faible nombre limite les possibilités de création, mais dans des messages d’Etat relativement court, sur des sujets qui n’ont rien à voir avec la littérature, ils peuvent bien s’appliquer. Il est peu vraisemblable que de tels symboles aient été employés, même s’il n’est pas exclu que certains mots soient symbolisés pour abréger la rédaction du texte, non pour limiter la taille du texte mais pour réduire un ou des mots employés fréquemment à un seul symbole. Expliquons : le texte et les dessins ont une unité telle que des mots ont pu être symbolisés par un seul caractère de la même manière que Gifford l’a fait. Gifford ne coupait pas les mots cryptographiés alors que le texte de notre manuscrit exprime bien des mots séparés par des blancs comme dans un texte classique.
Il est remarquablement intéressant que la forme graphique du nouvel alphabet n’ait pas de rapport avec la graphie des caractères dont ils sont la substitution. Le manuscrit Voynich serait-il ainsi un nouvel exercice d’un esprit éclairé ayant repris l’alphabet de Gifford pour ses besoins propres. Gifford est anglais, Roger Bacon aussi, mais il y a cependant deux siècles d’écart entre les deux hommes. S’il y a eu un lien sur cette idée de substitution graphique, qui a pu le prendre à l’autre si tant est qu’il y a eu un lien entre les deux.
Le français Rossignol au XVIe siècle exerce pendant 40 ans une influence considérable sur la cryptographie. Vers 1660, José Maximilien Brenckhorst, diplomate belge, imagine une méthode de chiffrement qui utilise simultanément le « carré de Vigenère » avec le système de Jules César.
Au cours de même siècle, le mathématicien milanais Jérôme Cardan qui travaillait sur les nombres complexes et les équations du troisième degré, s’est également consacré à la cryptographie. Il utilisa le message chiffré pour faire évoluer dynamiquement la clef de déchiffrement. Il s’agit, par exemple, d’enchaîner des décalages à une valeur issue elle-même du chiffré en formation (Jacques Stern). Il créa aussi un procédé de chiffrement original qui consistait à découper des petites fenêtres dans une feuille, puis d’appliquer cette feuille sur une autre, et d’écrire le message à cacher dans les fenêtres. Ensuite, il fallait enlever la feuille composée de fenêtres, et compléter les espaces laissés vides par des mots et des lettres qu’ils aient ou non un sens. Le décrypteur aura aussi un modèle de feuille à fenêtres qu’il appliquera sur le message, et cette feuille masquera le texte inutile. Cette technique est plus de la stéganographie, c’est à dire cacher un texte dans un texte plus vaste.
En 1663, Anathasius Kircher suggère la transformation du carré de Vigenère en remplaçant les alphabets littéraux par des alphabets numériques.
Nous nous arrêterons à cette période car les techniques de cryptographie ont ensuite beaucoup trop évolué pour pouvoir avoir été potentiellement utilisées par un auteur du XVe ou même du XVe siècle.
Les quelques données historiques que nous avons évoquées, n’ont qu’une valeur de montrer l’ancienneté des techniques de cryptographie. Les anglais, les français, les italiens ont été précurseurs dans cette période où le pouvoir a commencé à influencer les princes des Royaumes au delà des seules guerres d’invasion ou de conquête. Marie Stuart, reine d’Ecosse, en est le plus bel exemple, elle qui tout au long de sa vie « politique » a maitrisé le pouvoir et l’a construit en employant des messages chiffrés pour comploter contre la reine d’Angleterre Elizabeth.
Le XVe siècle a été peu fécond en cryptographie alors que le XVe siècle l’a été davantage. Ce siècle qui a donné naissance à la « Renaissance » a été celui aussi de l’ouverture entre nations, d’échanges, de commerce, et de stabilité un peu plus grande.
Le prochain chapitre, nouvelle pièce de notre puzzle, décrira les techniques de chiffrement d’avant 1700. Les systèmes restent parfois assez complexes. Alors si l’écriture du manuscrit était un code, il aurait fallu que l’auteur le maîtrise absolument parfaitement car l’écriture dans sa forme est claire et continue, sans marque d’hésitation. Certains caractères montrent une aisance dans l’écriture. Nous ne croyons pas probable l’utilisation d’un code complexe telle les disques de Cardan qui aurait nécessité une pause dans l’écriture des caractères, ce que nous ne trouvons pas.
LES CODES
Notre approche ici sera de bien connaître, sans cependant tomber dans une discussion trop technique, les différentes techniques de chiffrement, de codage, … d’encryption. Autant de termes qui qualifient une volonté séculaire voire millénaire de cacher un texte à des lecteurs qui n’en seraient pas destinataires. Ces techniques sont principalement issues du monde chrétien occidental. L’empire musulman a également contribué aux techniques cryptographiques, et les hindous, connaissent aussi le pouvoir du chiffre puisqu’un des arts que doivent posséder les femmes (dans le Kama-Sutra) est l’art de l’écriture secrète afin de cacher leurs liaisons.
Différentes méthodes ont été employées, dont certaines font appel à des compléments matériels pour aider le texte clair à passer dans une phase cryptée : les disques de cuivre, les matrices (pour écrire dans des emplacements pre-déterminés), les scytales (rubans autour d’un axe de diamètre prédéfini) …
L’exemple le plus célèbre d’analyse de déchiffrement se retrouve dans une nouvelle d’Edgar Allan Poe qui repose sur l’analyse des fréquences pour déchiffrer le texte secret. Cette méthode est connue, tout comme la simple substitution, qu’il y ait ou non un décalage dans les lettres dont on fait la substitution.
De manière schématique, l’écriture secrète, du moins celle que nous aborderons, recouvre soit la stéganographie, soit la cryptographie.
La stéganographie est un texte secret (texte en clair) caché dans un texte plus vaste, de telle sorte que la lecture du texte principal ne permette pas, sans clef, de découvrir, et donc de lire, le texte secret.
La cryptographie recouvre deux aspects : la transposition et la substitution. La substitution se subdivise en « code » (on change les mots) et en « chiffre » (on change les lettres). Dans cette opération, on remplace, en respectant l’ordre de succession, les lettres d’un texte clair par des unités de chiffrement, symboles, chiffres, lettres.
La transposition est une opération par laquelle, on déplace les unes par rapport aux autres, les lettres d’un texte clair. Les anagrammes sont un exemple de transposition.
Nous évoquerons donc un nombre assez important de techniques. Nous analyserons en fin de chapitre pour chacune des méthodes la possibilité que l’auteur ait pu l’utiliser de manière concrète et pratique dans la rédaction du manuscrit.
I) TRANSPOSITION SIMPLE
a) Transposition simple sans clef
Ce genre de procédé fait appel à une figure ou un dessin géométrique, un tableau, un canevas, bref, une trame de lecture, qui permet de lire un texte précédemment écrit selon ces formes géométriques.
E U I Y H U
L MN SR TO NC ET N
A C V I S
Le texte chiffré ici est «Le manuscrit Voynich est un ». Il s’agit d’une lecture sur la base d’une croix grecque, dans le sens des aiguilles d’une montre.
b) Transposition simple à tableau sans clef
Un exemple type de ce procédé est de créer des tableaux de lettres de 5 fois 5 (donc 25 lettres). On créera donc autant de tableaux de 25 lettres que le texte en clair est multiple de 25. On complétera par des lettres neutres pour faire le complément à 25 si le texte clair n’était pas un multiple de 25.
Exemple : « l’étude du manuscrit voynich permettra peut être de connaître le code secret employé ».
Nombre de lettres de cette phrase : 71, donc on aura 3 tableaux de 25 lettres
Les tableaux sont remplis en commençant en haut à droite de chaque carré, et en lisant par diagonale de droite vers la gauche et de haut gauche vers le bas droit.
| NDUEL | URERE | CDEER |
| IUUDT | ETATM | MRECL |
| YTSME | ODEPT | YPESO |
| CVVCA | ANETE | BELTE |
| PHIOR | TINCR | DCAOE |
Ainsi, en développé, le message sera :
NDEL IUUT YTSME CVVCA PHIOR
URERE ETATM ODEPT ANETE TINCR
CDEER MRECL YPESO BELTE DCAOE
Dans ce cas là, les lettres sont regroupées par paquet de 5. Mais ensuite, on peut provoquer un éclatement des lettres de manière aléatoire pour masquer la clef 5 fois 5. Un texte du genre « letudedumanus crit voy nichperme tt rapeutre deconnait relecodesecrete mploye » est relativement visible.
On peut de plus, sur les carrés, partir non plus du coin en haut à droite, mais d’un autre emplacement, qui peut lui aussi évoluer de manière ordonnée à la lecture des carrés suivants. On a donc là une cryptographie facile à mettre en œuvre, délicate à déchiffrer, mais comme toute méthode basée sur la transposition ou la substitution, faible à l’analyse des fréquences.
c) Clefs de transposition simple
En utilisant une clef numérique du style A=1, B=2, … Z=26, on arrive à codifier un texte en remplaçant les lettres par leur équivalent numérique. Bien sur, on peut prendre comme valeur initiale pour 1, non pas forcément A, mais toute autre lettre. Par exemple, J=1, K=2, L=3… I=26.
En utilisant non plus une forme linéaire, mais un tableau, il est possible de positionner un texte différemment.
Exemple : ceci est un livre sur le manuscrit Voynich
C E C I E 1 2 3 4 5
S T U N L 6 7 8 9 10
L I V R E 11 12 13 14 15
S U R L E 16 17 18 19 20
M A N U S 21 22 23 24 25
C R I T V 26 27 28 29 30
O Y N I C 31 32 33 34 35
H A B C D 36 37 38 39 40
Nous sommes partis conventionnellement de 1 en haut à droite, en suivant un ordre linéaire de gauche à droite, et de haut en bas. Nous aurions bien pu commencer la codification en partant du coin en bas à droite, et de remonter en suivant les diagonales, sur un axe bas/haut, et droite/gauche.
Pour l’opération de relèvement, on suit sur le tableau numérique un axe de progression logique, et on re-ecrit les lettres. Par exemple, on prend la première colonne qu’on lit de haut en bas parce qu’elle est impaire, et les colonnes paires sont lues de bas en haut.
On aura donc pour cet exemple :
1 6 11 16 21 26 31 36
37 32 27 22 17 12 7 2
3 8 13 18 23 28 33 38
39 34 29 24 19 14 9 4
5 10 15 20 25 30 35 40
Le texte est donc : CSLSMCOH AYRAUITE CUVRNINB CITULRNI ELEESVCD
Toute autre composition est bien sur possible à condition de bien connaître le déroulement des opérations.
L’utilisation d’une clef littérale peut se faire de la façon suivante.
Soit la clef suivante, avec comme première clef numérique N=1, M=2…
M A N U S C R I T V O Y N I C H
1 15 2 8 6 17 5 23 7 9 3 13 2 23 17 22
On peut codifier le texte suivant :
« il s’agit d’un texte ancien qui n’a jamais été à ce jour déchiffré »
M A N U S C R I T V O Y N I C H
1 15 2 8 6 17 5 23 7 9 3 13 2 23 17 22
I L S A G I T D U N T E X T E A
N C I E N Q U I N A J A M A I S
E T E A C E J O U R D E C H I F
F R
Le relèvement des colonnes peut commencer par exemple par la première colonne on l’on trouve la lettre A (ou bien sur tout autre lettre). Le chiffre est 15, donc impair. On prendra ensuite, à partir de la deuxième colonne, de gauche à droite, d’abord les colonnes à chiffre impair, puis ensuite, les colonnes paires.
Ainsi, le texte codé est :
LCTR IQE TUJ DIO UNU NAR TJD EAE TAH EII INEF SIE AEA GNC XMC ASF
On aurait pu compléter le tableau où il reste des cases vierges par des caractères neutres afin d’avoir des mots de longueur uniforme, de 4 lettres dans cet exemple.
II) LA SUBSTITUTION SIMPLE
L’alphabet a,c,c,d,e,f… x,y,z peut être remplacé des lettres qui se substitueraient à l’ordonnancement normal de l’alphabet.
Dans cet exemple, l’ordre de l’alphabet est linéaire mais commence non plus par A mais pas V.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
On pourrait composer un alphabet où on interverti les lettres deux à deux. Mais on pourrait aussi intervertir deux à deux les paires AB,CD, EF… (1), ou bien on peut jouer aussi sur des triplets : ABC deviendrait CAB, DEF serait FDE…
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B A D C F E H G J I L K N M P O R Q T S V U X W Z Y
On pourrait aussi prendre dans la suite des lettres de 1 à 26 d’abord les lettres de valeur impaire, puis après la 13e lettre, celles de valeur paire.
Une autre substitution possible serait de prendre l’ordre normal de l’alphabet en enlevant d’abord les voyelles et en les reportant à la fin, dans l’ordre inverse de leur apparition dans l’alphabet.
Si l’on continue sur des substitutions simples, l’alphabet substitué commencerait par un nom commun ne répétant aucune lettre comme par exemple PIANOS, puis en continuant l’alphabet par dernière lettre du mot clef…
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
P I A N O S T U V W X Y Z B C D E F G H J K L M N Q
On peut prendre non plus la dernière lettre du mot-clef, mais s’il est impair, la lettre centrale. Beaucoup de méthodes sont envisageables.
III) LA SUBSITUTION SIMPLE A REPRESENTATIONS MULTIPLES
Dans cette situation, l’alphabet ordinaire est modifié de telle sorte d’avoir un nouvel alphabet, avec par exemple l’utilisation d’un mot clef, mais une lettre de l’alphabet clair peut donner plusieurs unités cryptographiques, mais chaque unité cryptographique ne donnera qu’une lettre dans l’alphabet clair.
Le principe n’est pas forcément compliqué, ni le chiffrement. Par contre, pour tenter de déchiffrer le code sans la matrice clef, les difficultés sont importantes.
A/S F/E D/Z G/B R/O
H/B b p h i r
W/C e y q f j
P/T d z a g k
I/U x c n t s
J/K v o m u l
Dans cette matrice-clef, la lettre B peut être chiffrée par 8 couples : HA, HS, BA, BS, AH, AB, SH, SB
En fonction des couples situés en abscisses et en ordonnées, on peut arriver à ce qu’un lettre en clair puisse avoir de 2 à 16 représentations codées. Au delà de huit, le chiffrement reste acceptable mais ralentit l’écriture du code. D’autres méthodes permettent de varier le nombre de couples codés pour chaque lettre en clair.
Chaque lettre en clair donnant un couple de lettres en code, on en déduit facilement que le texte codé sera deux fois plus long. L’analyse des fréquences sera mise à mal car lors de l’écriture du code, on peut prendre au choix un couple de lettres, par exemple toujours le premier. Ou bien, à chaque représentation d’une lettre en clair, on prend d’abord le premier couple dans l’alphabet chiffré, puis à la seconde occurrence de la même lettre, le second couple et ainsi de suite. Il faut donc d’une part connaître la matrice initiale, et la façon de choisir les couples.
II) LA SUBSTITUTION A DOUBLE CLEF
Dans les exemples ci-dessus, la substitution était simple : on employait un alphabet pour passer du texte clair au texte codé.
Il s’agir maintenant de voir les méthodes qui conduisent à employer non pas un alphabet mais plusieurs afin de compliquer le déchiffrement.
Il faudra alors deux éléments importants dans la rédaction du message à coder, utilisés bien sûr dans l’opération de déchiffrement :
* la loi de formation des alphabets de substitution
* l’ordre d’emploi de ces alphabets
C’est le « carré de Vigenère » qui sera développé ici, bien que le napolitain Porta ait découvert peu avant ce procédé. Porta utilisa le latin, donc 22 lettres, alors que Vigenère pris les 26 lettres de l’alphabet. Dans le cadre de notre étude du manuscrit, il pourrait être envisageable que le chiffre utilisé fut basé sur l’alphabet latin.

Blaise de Vigenère
(1523-1596)

La formation de ce carré est simple : la première reprend l’ordre alphabétique en partant de A, la seconde en partant de B et ainsi de suite.
Pour chiffrer par exemple le texte «ceci est un livre sur le manuscrit», avec la clef VOYNICH, nous avons la formation suivante :
V O Y N I C H V O Y N I C H V O Y N I C H V O Y N I C H
c e c i e s t u n l i v r e s u r l e m a n u s c R i t
X S A V M U A Q B J V D T L O I P Y M O H J I Q F Z N A
Pour la première lettre « c », on la colonne V, puis on prend la ligne avec « c », et à l’intersection, nous avons la première lettre codée « X »….
Dans cette cryptographie, même si la lecture du tableau à double entrée est simple et peu contraignante, tout réside dans la clef. Plus la clef est longue, plus le texte sera difficile à déchiffrer. Bien sûr, si la clef est égale en longueur au texte lui-même, rien ne sert de crypter puisqu’il faut envoyer deux longues informations.
On peut par contre convenir que le mot « VOYNICH » de la première ligne ne se répète par de la même manière, mais par rotation, par exemple « OYNICHV », puis la troisème répétition « YNICHVO »… on utilise ainsi le décalage qui a servi dans le tableau ci-dessus. Pour compliquer l’utilisation de la clef, on peut faire évoluer la clef au delà du simple décalage, en prenant comme clef, le premier mot suivi des x premières lettres déchiffrées,x étant égal à la longueur de la clef. Le début de la clef serait ainsi dans notre exemple : « VOYNICHCECIES ». Suivant la longueur du texte, il est possible de décrire un processus d’écriture de la clef qui puisse d’une part se retenir suivant une convention particulière, et d’autre part être stable pour éviter d’être déchiffrée.
D’autre part, l’utilisation de l’alphabet dans le tableau peut être remplacé par un mot clef à la suite duquel on reprend la continuation de l’alphabet en omettant les lettres reprises dans le mot clef. Exemple des 3 premières lignes du tableau de Vigenère en prenant cette nouvelle contrainte ; le mot clef du tableau est « VOYNICH ». Elle peut être naturellement différente du mot clef de déchiffrement.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
a V O Y N I C H J K L M P Q R S T U W X Z A B D E F G
b O Y N I C H J K L M P Q R S T U W X Z A B D E F G V
c Y N I C H J K L M P Q R S T U W X Z A B D E F G V O
On pourrait continuer cette discussion bien au delà des techniques que nous avons évoquées en compliquant les possibilités d’encryption, en essayant d ‘établir par exemple un process de chiffrement étape par étape. Le physicien italien Giovanni Battista Della Porta fut l'inventeur du premier système littéral à double clef, c'est-à-dire le premier chiffre pour lequel on change d'alphabet à chaque lettre. Ce système polyalphabétique était extrêmement robuste pour l'époque, à tel point que beaucoup considèrent Porta comme le "père de la cryptographie moderne". Della Porta a inventé son système de chiffrement en 1563, et il a été utilisé avec succès pendant trois siècles. Porta emploie 11 alphabets différents et réversibles qu'il désigne, comme on le voit dans la figure ci-dessous, par AB, CD, EF, etc.
On pourrait se demander si à force de compliquer le chiffrement, il serait possible de le déchiffrer. Quasiment tous les algorithmes classiques sont symétriques et réversibles. Ce n’est que depuis peu que les développements récents de la cryptographie s’oriente vers des schémas non réversibles, dit asymétriques, dans lesquels la composante mathématique est importante.
Que ce manuscrit ait été écrit au XVe siècle ou au XVIe siècle, nous n’avons que deux possibilités : ou le texte est vraiment chiffré ou il ne s’agit que d’un brillant exercice graphique, œuvre d’un fou littéraire – que cette expression ne soit là bien sûr pas péjorative –.
Si le texte est chiffré, il peut l’être suivant les méthodes classiques de chiffrement telles que nous l’avons présenté ci-dessus, même si le process d’encryption est beaucoup plus compliqué que notre présentation, ou être crypté suivant un nouvel alphabet qui aurait alors une nouvelle grammaire, une nouvelle sémantique.
La question ici à se poser est de savoir, pour le cas où le texte serait chiffré suivant les méthodes classiques, si un auteur du XVe ou du XVIe siècle aurait pu se livrer à un exercice si compliqué.
Nous voudrions d’abord ajouté que les esprits cultivés de ces périodes, loin des voitures et des télévisions qui consomment beaucoup de temps au gens de notre époque, avaient non seulement du temps, mais étaient cultivés dans beaucoup de disciplines, à une époque où la spécialisation productive n’était pas encore apparue. La rapide présentation de Roger Bacon nous montre la diversité des connaissances qu’avaient les lettrés de cette période, en particulier les théologiens, qu’ils proviennent ou non des universités (Padoue, Oxford, Paris, Cologne…). Ce spectre très large de connaissances, que nous ne retrouvons plus de nos jours, ou trop peu comme Umberto Eco, ou il y a encore quelques années avec JL Borgès qui tous deux ont (eu) un savoir encyclopédique, est une donnée importante : ce qui nous semblerait complexe ne l’était pas pour ces personnes qui avaient une vraie connaissance du monde, qu’elle soit d’ailleurs vraie ou non. Leur vision du monde était globale.
Ensuite, il nous semble important de préciser que si une méthode de chiffrement compliquée a été réellement utilisée, il ne s’agit que de 260 pages, lesquelles ne sont pas remplies uniquement par du texte. Ce manuscrit, propre, sans rature, a pu être aussi le résultat final et la recopie d’un brouillon reprenant un process de codage savant.
Ecrire une page en utilisant le carré de Vigenère, même avec une clef dynamique (c’est- à-dire évoluant avec l’encodage) est relativement rapide. Il faut simplement bien délimiter le process. Ce manuscrit n’est pas l’œuvre d’une vie. Il peut avoir été rédigé à la fin de la vie de l’auteur, mais ne lui a certainement pas pris toute sa vie. Pour une raison aussi de cohérence dans l’écriture. Aucun tremblement dans l'écriture.
Certains livres ont pris pour être écrit des années entières (je pense notamment aux Nouvelles Impressions d’Afrique de Raymond Roussel), ou de Finnegans Wake de James Joyce, mais ceci est toutefois d'une autre nature.
Concernant les méthodes de chiffrement que nous avons présentées, nous avons l’intuition qu’elles ont pu être utilisées par l’auteur. Roger Bacon a anagrammatisé la « recette » de la poudre à canon ! Plaçons nous maintenant sur une phrase du manuscrit avec une suite de lettres incohérentes a priori. S’il s’agissait d’anagrammes ? Par ligne ? Par demie-ligne ? Dans quelle langue ? Pour des raisons pratiques, les caractères graphiques de type « arabesques » peuvent représenter des groupes de lettres, rendant ainsi plus difficile le déchiffrement, ou des caractères vides de sens.
Quoi qu’il en soit, cette méthode est faible face à l’analyse des fréquences des lettres. Nous y reviendrons par la suite.
